Material Point Method
Divergence Theorem #
\[\int_{\partial V} \boldsymbol{u}\cdot\boldsymbol{n}\ dS=\int_V\nabla\cdot\boldsymbol{u}\ dV\]where $\boldsymbol{u}$ is a vector field defined in volume $V$, $\boldsymbol{n}$ is the outward facing normal of boundary $\partial V$.
Convection Thereom #
Following notation in mpm course:
\[\begin{align} \frac{d}{dt}\int_{\Omega_t}f(\boldsymbol{x},t)dv&=\frac{d}{dt}\int_{\Omega_0}f(\Phi(\boldsymbol{X},t),t)JdV\\ &=\int_{\Omega_0}\frac{df(\Phi(\boldsymbol{X},t),t)}{dt}JdV+\int_{\Omega_0}f(\Phi(\boldsymbol{X},t),t)\frac {dJ}{dt}dV\\ &=\int_{\Omega_0}(\frac{\partial f}{\partial t}|_{(\Phi(\boldsymbol{X},t),t)}+\frac{\partial f}{\partial \boldsymbol{x}}|_{(\Phi(\boldsymbol{X},t),t)}\frac{\partial \Phi}{\partial t}|_{(\boldsymbol{X},t)}) JdV+\int_{\Omega_0}f(\Phi(\boldsymbol{X},t),t)(\nabla\cdot \boldsymbol{u})JdV\\ &=\int_{\Omega_0}(\frac{\partial f}{\partial t}|_{(\Phi(\boldsymbol{X},t),t)}+\nabla f|_{(\Phi(\boldsymbol{X},t),t)}\cdot \boldsymbol{U}|_{(\boldsymbol{X},t)}) JdV+\int_{\Omega_0}f|_{(\Phi(\boldsymbol{X},t),t)}(\nabla\cdot \boldsymbol{u})|_{(\Phi(\boldsymbol{X},t),t)}JdV\\ &=\int_{\Omega_t}(\frac{\partial f}{\partial t}|_{(\boldsymbol{x},t)}+\nabla f|_{(\boldsymbol{x},t)}\cdot \boldsymbol{u}|_{(\boldsymbol{x},t)}) dv+\int_{\Omega_t}f|_{(x,t)}(\nabla\cdot \boldsymbol{u})|_{(x,t)}dv\\ &=\int_{\Omega_t}\left(\frac{\partial f}{\partial t}+\nabla f\cdot \boldsymbol{u} + f(\nabla\cdot \boldsymbol{u})\right)dv\\ &=\int_{\Omega_t}\left(\frac{\partial f}{\partial t}+\nabla\cdot (f\boldsymbol{u})\right)dv\\ &=\int_{\Omega_t}\frac{\partial f}{\partial t}dv+\int_{\partial\Omega_t}f\boldsymbol{u}\cdot \boldsymbol{n}\ dS \end{align}\]where $f$ is a scalar field defined on eulerian coordinate $x$. To be more specific, $f$ is a physical quantity that defined by “$f$ per unit volume”, for example, the density. If $f$ is defined by “$f$ per unit mass”, for example, acceleration is defined by “force per unit mass”, then we have another convection identity
\[\frac{d}{dt}\int_{\Omega_t}\rho f(\boldsymbol{x},t)dv=\int_{\Omega_t}\left(\frac{\partial \rho f}{\partial t}+\nabla\cdot (\rho f\boldsymbol{u})\right)dv\]where $\rho$ is the density.
In the 6th equality, we use $\boldsymbol{U}(\boldsymbol{X},t)=\boldsymbol{u}(\Phi(\boldsymbol{X},t),t)$
In the 8th equality, we use divergence theorem
In the 3rd equality, we use $dJ/dt={\rm div}(\boldsymbol{u})J$
Derivative of a determinant #
\[\frac{dJ}{dt}=\frac{d\left|F\right|}{dt}=\left|\begin{matrix} dr_{0}/dt\\ r_1\\ r_2 \end{matrix}\right|+\left|\begin{matrix} r_0\\ dr_{1}/dt\\ r_2 \end{matrix}\right|+\left|\begin{matrix} r_0\\ r_1\\ dr_2/dt \end{matrix}\right|\]where $r_i=(\partial x_i/\partial X_0\quad\partial x_i/\partial X_1\quad…\quad\partial x_i/\partial X_{n-1})$ and $dr_i/dt=(\partial u_i/\partial X_0\quad\partial u_i/\partial X_1\quad…\quad\partial u_i/\partial X_{n-1})$. Notice that we have following relation
\[\partial u_0/\partial X_0=\frac{\partial u_0}{\partial x_0}\frac{\partial x_0}{\partial X_0}+\frac{\partial u_0}{\partial x_1}\frac{\partial x_1}{\partial X_0}+\frac{\partial u_0}{\partial x_2}\frac{\partial x_2}{\partial X_0}\]So the first term can be expanded as
\[\left|\begin{matrix} dr_{0}/dt\\ r_1\\ r_2 \end{matrix}\right|=\frac{\partial u_0}{\partial x_0}\left|\begin{matrix}r_0\\r_1\\r_2\end{matrix}\right|+\frac{\partial u_0}{\partial x_1}\left|\begin{matrix}r_1\\r_1\\r_2\end{matrix}\right|+\frac{\partial u_0}{\partial x_2}\left|\begin{matrix}r_2\\r_1\\r_2\end{matrix}\right|=\frac{\partial u_0}{\partial x_0}{\rm det}(F)\]It further simplies to
\[\frac{dJ}{dt}=\frac{\partial u_0}{\partial x_0}{\rm det}(F)+\frac{\partial u_1}{\partial x_1}{\rm det}(F)+\frac{\partial u_2}{\partial x_2}{\rm det}(F)=(\nabla\cdot\boldsymbol{u})J\]Conservation of Mass #
Using convection theorem and subsitituting density into scalar field $f$, we have
\[\frac{d}{dt}\int_{\Omega_t}\rho dv=0=\int_{\Omega_t}\left(\frac{\partial \rho}{\partial t}+\nabla \rho\cdot \boldsymbol{u} + \rho(\nabla\cdot \boldsymbol{u})\right)dv=\int_{\Omega_t}\left(\frac{D \rho}{D t}+\rho(\nabla\cdot \boldsymbol{u})\right)dv\]This equation holds for any $\Omega_t$. So we further have
\[\frac{D \rho}{D t}+\rho(\nabla\cdot \boldsymbol{u})=0\]which is equation of conservation of mass. A positive value of the divergence, is associated with an expansive flow, thereby reducing local density.
Conservation of Momentum #
The momentum of a fluid is defined to be $\rho \boldsymbol{u}$, per unit volume. Then the total momentum is
\[\int_{\Omega_t}\rho(\boldsymbol{x},t)\boldsymbol{u}(\boldsymbol{x},t)dv\]The conservation is expressed as
\[\begin{align} \frac{d}{dt}\int_{\Omega_t}\rho(\boldsymbol{x},t)\boldsymbol{u}(\boldsymbol{x},t)dv&=\frac{d}{dt}\int_{\Omega_0}\rho(\Phi(\boldsymbol{X},t),t)\boldsymbol{u}(\Phi(\boldsymbol{X},t),t)JdV\\ &=\frac{d}{dt}\int_{\Omega_0}\rho(\Phi(\boldsymbol{X_0},t),t)\boldsymbol{u}(\Phi(\boldsymbol{X},t),t)dV\\ &=\int_{\Omega_0}\rho(\Phi(\boldsymbol{X_0},t),t)\frac{D\boldsymbol{u}}{Dt}|_{(\Phi(\boldsymbol{X},t),t)}dV\\ &=\int_{\Omega_0}R_0\boldsymbol{A}dV=\int_{\Omega_t}\rho\boldsymbol{a}dv\\ \end{align}\]where $\boldsymbol{A}(\boldsymbol{X},t)=\partial \boldsymbol{U}/\partial t=D\boldsymbol{u}/Dt=\boldsymbol{a}(\boldsymbol{x},t)$. The applied forces are expressed as
\[\int_{\Omega_t}\boldsymbol{f^{ext}}dv+\int_{\partial\Omega_t}\boldsymbol{\sigma}\boldsymbol{n}ds=\int_{\Omega_t}(\boldsymbol{f^{ext}}+\nabla\cdot\boldsymbol{\sigma})dv\]So the conservation in eulerian view is
\[\rho\boldsymbol{a}=\boldsymbol{f^{ext}}+\nabla\cdot\boldsymbol{\sigma}\]In lagrangian we have
\[R_0\boldsymbol{A}=\nabla\cdot\boldsymbol{P}+J\boldsymbol{F^{ext}}\]since $\int_{\partial\Omega_t}\boldsymbol{\sigma}\boldsymbol{n}ds=\int_{\partial\Omega_0}J\boldsymbol{\sigma}F^{-T}\boldsymbol{N}dS=\int_{\partial\Omega_t}\boldsymbol{P}\boldsymbol{N}dS$. Here $\boldsymbol{P}=J\boldsymbol{\sigma}\boldsymbol{F}^{-T}$ is the first Piola Kirchoff stress tensor.
The Cauchy Stress Tensor #
Following Solid Mechanics Theory, a traction vector at a point on a virtual surface passing through the point is defined by
\[\boldsymbol{t}=\lim\limits_{\Delta A\rightarrow 0}\frac{\Delta \boldsymbol{F}}{\Delta A}\]Where $\Delta A$ is the area of the virtual surface surrounding the point. It can be seen that every point on this surface will experience an internal force, and so there is a internal force distribution on this surface. $\Delta F$ means the sum of these forces on the surface. So actually, the traction vector means the average force on this virtual surface.
Notice that the traction is not necessary to be aligned with surface normal. That is, the traction not only has a component perpendicular to the surface (which results in a stretch or compression), but also has a component parallel to the surface (which results in a shearing effect).
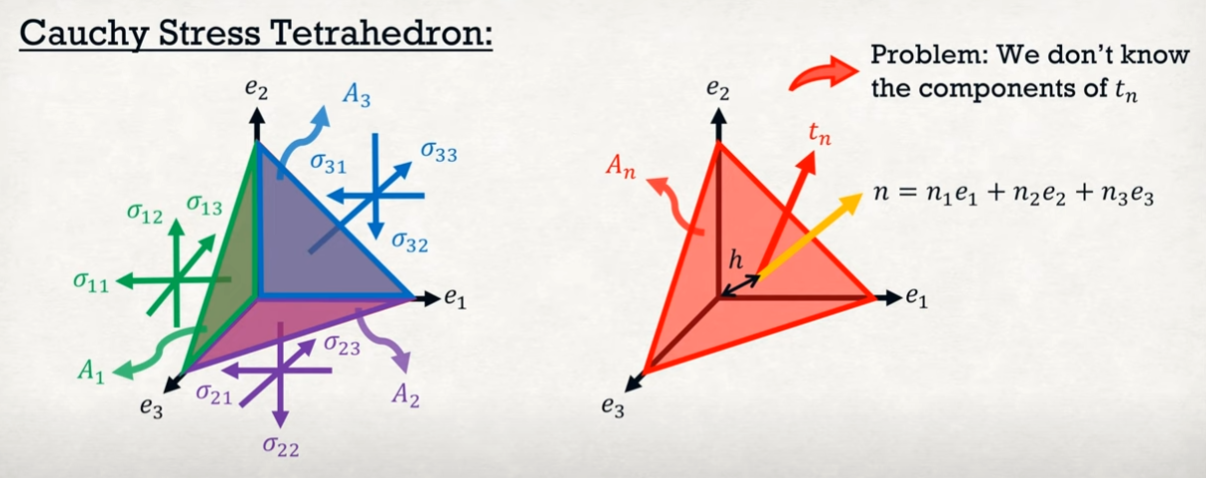
Now we choose $\boldsymbol{e_1,e_2,e_3}$ to be world basis vectors. Consider a infinitesimal tetrahedron surrounding a point. It has 4 faces. Since the tetrahedron is infinitesimal small, the traction on each surface, is same with the traction at the interpoint with the same surface orientation. As mentioned above, every traction can be represented as $\boldsymbol{t_i}=\sigma_{i1}\boldsymbol{e_1}+\sigma_{i2}\boldsymbol{e_2}+\sigma_{i3}\boldsymbol{e_3},i=1,2,3$. Now we want to calculate $\boldsymbol{t_4}$. We have following equilibrium equation
\[\sum F_{e_1}=-\sigma_{11}A_1-\sigma_{21}A_2-\sigma_{31}A_3+t_{n_1}A_n+mg_1=ma_1\]And we will finally get
\[\begin{align} t_{n1}&=\sigma_{11}n_1+\sigma_{21}n_2+\sigma_{31}n_3\\ t_{n2}&=\sigma_{12}n_1+\sigma_{22}n_2+\sigma_{32}n_3\\ t_{n3}&=\sigma_{13}n_1+\sigma_{23}n_2+\sigma_{33}n_3 \end{align}\]That is the relationship between traction $\boldsymbol{t}$, surface normal $\boldsymbol{n}$ and cauchy stress tensor $\boldsymbol{\sigma}$ (symmetric)
\[\boldsymbol{t}=\boldsymbol{\sigma}^T\boldsymbol{n}=\boldsymbol{\sigma}\boldsymbol{n}\]- $\boldsymbol{\sigma}$ is symmetric
- There exists a coordinate system where $\boldsymbol{\sigma}$ is diagonal (principal stress)
To conclude, we have
conservation of mass (in case that there is no mass sink or add source)
Eulerian
\[\frac{D \rho}{D t}+\rho(\nabla\cdot \boldsymbol{u})=0\]Lagrangian
\[RJ=R_0\]conservation of momentum
Eulerian
\[\rho\boldsymbol{a}=\nabla\cdot\boldsymbol{\sigma}+\boldsymbol{f^{ext}}\]Lagrangian
\[R_0\boldsymbol{A}=\nabla\cdot\boldsymbol{P}+J\boldsymbol{F^{ext}}\]
Weak Form #
Consider an arbitrary test function $\boldsymbol{Q}(\boldsymbol{X},t):\Omega_0\rightarrow R^d$ and its eulerian counter part $\boldsymbol{q}(\boldsymbol{x},t):\Omega_t\rightarrow R^d$ where $\boldsymbol{Q}(\boldsymbol{X},t)=\boldsymbol{q}(\Phi(\boldsymbol{X},t),t)$. Since we have
\[R_0\boldsymbol{A}=\nabla\cdot\boldsymbol{P}+J\boldsymbol{F^{ext}}\]so we further get following equation if we ignore external force for simplicity
\[\int_{\Omega_0}\boldsymbol{Q}\cdot (R_0\boldsymbol{A})dV=\int_{\Omega_0}\boldsymbol{Q}\cdot (\nabla\cdot\boldsymbol{P})dV\]where $\boldsymbol{P}=P_{\alpha\beta}$ and
\[\begin{align} \boldsymbol{Q}\cdot(\nabla\cdot\boldsymbol{P})&=\boldsymbol{Q}\cdot\begin{pmatrix} \nabla\cdot(P_{11},P_{12},P_{13})^T\\ \nabla\cdot(P_{21},P_{22},P_{23})^T\\ \nabla\cdot(P_{21},P_{32},P_{33})^T\\ \end{pmatrix}=\boldsymbol{Q}\cdot\begin{pmatrix} P_{1j,j}\\ P_{2j,j}\\ P_{3j,j} \end{pmatrix}=Q_iP_{ij,j}\\ \nabla\cdot(\boldsymbol{P^TQ})&=(P^TQ)_{j,j}=(P^T_{ji}Q_{i})_{,j}=(P_{ij}Q_{i})_{,j}=Q_iP_{ij,j}+P_{ij}Q_{i,j} \\ \boldsymbol{Q}\cdot(\nabla\cdot\boldsymbol{P})&=\nabla\cdot(\boldsymbol{P^TQ})-P_{ij}Q_{i,j}=\nabla\cdot(\boldsymbol{P^TQ})-P_{ij}Q_{i,j} \end{align}\]So
\[\begin{align} \int_{\Omega_0}\boldsymbol{Q}\cdot (R_0\boldsymbol{A})dV&=\int_{\Omega_0}\boldsymbol{Q}\cdot (\nabla\cdot\boldsymbol{P})dV\\ &=\int_{\Omega_0}\nabla\cdot(\boldsymbol{P^TQ})dV-\int_{\Omega_0}P_{ij}Q_{i,j}dV\\ &=\int_{\partial\Omega_0}(\boldsymbol{P^TQ})\cdot\boldsymbol{N}dS-\int_{\Omega_0}P_{ij}Q_{i,j}dV\\ &=\int_{\partial\Omega_0}\boldsymbol{Q^TPN}dS-\int_{\Omega_0}P_{ij}Q_{i,j}dV\\ \end{align}\]where
\[Q_{i,j}=\frac{\partial Q_i}{\partial X_j}=\frac{\partial q_i}{\partial x_k}\frac{\partial x_k}{\partial X_j}=\frac{\partial q_i}{\partial x_k}F_{kj}=q_{i,k}F_{kj}\]Push forward we have
\[\begin{align} \int_{\Omega_t}\boldsymbol{q}\cdot (\rho\boldsymbol{a})dv&=\int_{\partial\Omega_0}\boldsymbol{Q^TT}dS-\int_{\Omega_t}P_{ij}q_{i,k}F_{kj}dV\\ &=\int_{\partial\Omega_0}\boldsymbol{Q^T}\boldsymbol{F}^{int}-\int_{\Omega_t}q_{i,k}\frac{1}{J}P_{ij}F_{kj}dv\\ &=\int_{\partial\Omega_t}\boldsymbol{q^T}\boldsymbol{f}^{int}-\int_{\Omega_t}q_{i,k}\sigma_{ik}dv\\ &=\int_{\partial\Omega_t}\boldsymbol{q^T}\boldsymbol{t}ds-\int_{\Omega_t}{\rm tr}(\nabla\boldsymbol{q\ \sigma})dv\\ &=\int_{\partial\Omega_t}\boldsymbol{q^T}\boldsymbol{\sigma n}ds-\int_{\Omega_t}{\rm tr}(\nabla\boldsymbol{q\ \sigma})dv\\ &=\int_{\partial\Omega_t}q_it_ids-\int_{\Omega_t}q_{i,k}\sigma_{ik}dv \end{align}\]Evolve of Internal Force #
\[\frac{\partial F(\boldsymbol{X},t)}{\partial t}=\frac{\partial(\partial \boldsymbol{x}/\partial \boldsymbol{X})}{\partial t}=\frac{\partial(\partial \boldsymbol{x}/\partial t)}{\partial \boldsymbol{X}}=\frac{\partial \boldsymbol{v}(\Phi(\boldsymbol{X},t))}{\partial \boldsymbol{X}}=\frac{\partial \boldsymbol{v}}{\partial \boldsymbol{x}}\frac{\partial\boldsymbol{x}}{\partial \boldsymbol{X}}=\frac{\partial \boldsymbol{v}}{\partial \boldsymbol{x}}F\]Say particles have a deformation gradient of $F_p^n$ at time $t^n$, then we have
\[\frac{F_p^{n+1}-F_p^n}{\Delta t}=\frac{\partial \boldsymbol{v}^{n+1}}{\partial \boldsymbol{x}}F_p^n\\ F_p^{n+1}=(\boldsymbol{I}+\Delta t\frac{\partial \boldsymbol{v}^{n+1}}{\partial \boldsymbol{x}})F_p^n\]where
\[\begin{align} \frac{\partial \boldsymbol{v}^{n+1}}{\partial \boldsymbol{x}}&=\frac{\partial\sum_iN(\boldsymbol{x}-\boldsymbol{x}_i^n)\boldsymbol{\widetilde{v}}_i^{n+1}}{\partial\boldsymbol{x}}=\sum\limits_i\boldsymbol{\widetilde{v}}_i^{n+1}(\nabla w_{ip})^T \end{align}\]Derivative of a scalar-vector function #
Consider a scalar function $f:R^d\rightarrow R$ and a constant vector $\boldsymbol{v}\in R^d$.
\[\frac{\partial f\boldsymbol{v}}{\partial \boldsymbol{x}}=(fv)_{i,j}=f_{,j}v_i+fv_{i,j}=f_{,j}v_i=\boldsymbol{v}(\nabla f)^T\]So,
\[F_p^{n+1}=(\boldsymbol{I}+\Delta t\sum\limits_i\boldsymbol{\widetilde{v}}_i^{n+1}(\nabla w_{ip})^T)F_p^n\]Now, we want to identify how much stress does grid node has experienced. To figure out that, we need to define a energy function represented as $\boldsymbol{x}_i$. If the grid node $\boldsymbol{x_i}$ can move virtually to $\hat{\boldsymbol{x}_i}=\boldsymbol{x_i}+\Delta t\boldsymbol{\widetilde{v}_i^{n+1}}$, then the elastic energy can be represented as a function of $\hat{\boldsymbol{x}_i}$
\[e(\hat{\boldsymbol{x}})=\sum_p\psi(F_p(\hat{\boldsymbol{x}}))V_p^0\]where $\hat{\boldsymbol{x}}$ is the assembled vector of all Eulerian $\hat{\boldsymbol{x}_i}$. Here we think of the deformation gradient as a function of $\hat{\boldsymbol{x}}$.
This is because we are temporarily thinking of the motion of the material as defined in terms of the $\boldsymbol{X}_i=\Phi^{-1}(\boldsymbol{x}_i,t)$ and $\hat{\boldsymbol{x}_i}$. So,
\[F_p(\hat{\boldsymbol{x}})=(\boldsymbol{I}+\sum_i\boldsymbol(\hat{\boldsymbol{x}_i}-\boldsymbol{x}_i)(\nabla w_{ip})^T)F_p^n\]Then
\[\begin{align} -\boldsymbol{f}_{i}&=\frac{\partial e(\hat{\boldsymbol{x}})}{\partial \hat{\boldsymbol{x}_i}}=\frac{\partial e(\hat{\boldsymbol{x}})}{\partial F_p(\hat{\boldsymbol{x}})}\frac{\partial F_p(\hat{\boldsymbol{x}})}{\partial \hat{\boldsymbol{x}_i}}\\&=\sum\limits_pP_p^{n+1}V_p^0\frac{\partial F_p(\hat{\boldsymbol{x}})}{\partial \hat{\boldsymbol{x}_i}}\\ -\boldsymbol{f}_{i\alpha}&=\sum\limits_{p}\sum\limits_{\beta\gamma}P_{p\beta\gamma}^{n+1}V_p^0\frac{\partial F_{p\beta\gamma}(\hat{\boldsymbol{x}})}{\partial \hat{\boldsymbol{x}}_{i\alpha}} \end{align}\]where
\[\begin{align} \frac{\partial F_p(\hat{\boldsymbol{x}})}{\partial \hat{\boldsymbol{x}_i}}&=\frac{\partial \left(\sum_j\hat{\boldsymbol{x}}_j(\nabla w_{jp})^TF_p^n\right)}{\partial \hat{\boldsymbol{x}_i}}=\frac{\partial \left(\hat{\boldsymbol{x}}_i(\nabla w_{ip})^TF_p^n\right)}{\partial \hat{\boldsymbol{x}_i}}\\ \frac{\partial F_{p\beta\gamma}(\hat{\boldsymbol{x}})}{\partial \hat{\boldsymbol{x}}_{i\alpha}}&=\frac{\partial \left(\hat{\boldsymbol{x}}_{i\beta}\sum_{\epsilon}(\nabla w_{ip})^T_\epsilon F_{p\epsilon\gamma}^n\right)}{\partial \hat{\boldsymbol{x}}_{i\alpha}}=\delta_{\beta\alpha}\sum_{\epsilon}(\nabla w_{ip})^T_\epsilon F_{p\epsilon\gamma}^n \end{align}\]Derivative of a outer-product function #
Consider a constant vector $\boldsymbol{v}\in R^d$
\[\frac{\partial \boldsymbol{xv^T}}{\partial \boldsymbol{x}}=(xv)_{ij,k}=(x_iv_j)_{,k}=x_{i,k}v_j=\delta_{i,k}v_j\]So
\[-\boldsymbol{f}_{i\alpha}=\sum\limits_{p}\sum\limits_{\gamma}P_{p\alpha\gamma}^{n+1}V_p^0\sum_{\epsilon}(\nabla w_{ip})^T_\epsilon F_{p\epsilon\gamma}^n\]In APIC, we use
\[C_p^{n+1}=\sum\limits_i\boldsymbol{\widetilde{v}}_i^{n+1}(\nabla w_{ip})^T=\sum\limits_iw_{ip}\boldsymbol{\widetilde{v}}_i^{n+1}((D_p^n)^{-1}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n))^T\]It is also mentioned in APIC(JCP-version): page 23, paragraph 1.
So
\[F_p^{n+1}=(\boldsymbol{I}+\Delta tC_p^{n+1})F_p^n\]Now, the nodal force comes to
\[\begin{align} -\boldsymbol{f_i}&=\frac{\partial e(\hat{\boldsymbol{x}})}{\partial \hat{\boldsymbol{x}_i}}=\sum_pV_p^0\frac{\partial \psi(F_p(\hat{\boldsymbol{x}}))}{\partial \hat{\boldsymbol{x}_i}}\\ &=\sum_pV_p^0\frac{\partial \psi(F_p)}{\Delta t\ \partial \boldsymbol{v}_i}\\ &=\sum_p\frac{V_p^0}{\Delta t}\frac{\partial \psi(F_p)}{\partial F_p}\frac{\partial F_p}{\partial C_{p}}\frac{\partial C_p}{\partial \boldsymbol{v}_i}\\ &=\sum_p\frac{V_p^0}{\Delta t}P_p(F_p^{})\left(\Delta t (F_p^n)^T\right)\left(\frac{4}{\Delta x^2}w_{ip}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n)\right)\\ &=\sum_p\frac{4}{\Delta x^2}V_p^0P_p(F_p^{})(F_p^n)^Tw_{ip}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n) \end{align}\]the grid node positions $\boldsymbol{\hat{x}}_i$ are simply a function of grid node velocities $\boldsymbol{\widetilde{v}}_i$. The explicit force is simply the force assuming zero grid motion, that is,
\[P_p(F_p(\hat{\boldsymbol{x}}))=P_p(F_p({\boldsymbol{x}}))=P_p(F_p^n)=P_p^n\]Then
\[-\boldsymbol{f_i}=\sum_p\frac{4}{\Delta x^2}V_p^0P_p^{n}(F_p^n)^Tw_{ip}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n)\]Meanwhile, we have
\[\begin{align} dv&=JdV\\ \boldsymbol{ds}\cdot\boldsymbol{dl_3}&=J\boldsymbol{dS}\cdot\boldsymbol{dL_3}\\ \boldsymbol{ds}\cdot F\boldsymbol{dL_3}&=J\boldsymbol{dS}\cdot\boldsymbol{dL_3}\\ \boldsymbol{ds}^TF\boldsymbol{dL_3}&=J\boldsymbol{dS}^T\boldsymbol{dL_3}\\ \boldsymbol{ds}^TF&=J\boldsymbol{dS}^T\\ \boldsymbol{ds}&=JF^{-T}\boldsymbol{dS}\\ \end{align}\]and
\[\begin{align} \boldsymbol{t}ds&=\boldsymbol{T}dS\\ \sigma\boldsymbol{n}ds&=P\boldsymbol{N}dS\\ \sigma\boldsymbol{ds}&=P\boldsymbol{dS}\\ \sigma JF^{-T}\boldsymbol{dS}&=P\boldsymbol{dS}\\ J\sigma F^{-T}&=P\\ \sigma&=\frac{1}{J}PF^T\\ \end{align}\]So the nodal force can be rewritten as
\[\begin{align} -\boldsymbol{f_i}&=\sum_p\frac{4}{\Delta x^2}V_p^0P_p^{n}(F_p^n)^Tw_{ip}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n)\\ &=\sum_p\frac{4}{\Delta x^2}J^n_pV_p^0\sigma_p^nw_{ip}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n)\\ \end{align}\]why
\[C_p^{n+1}=\sum\limits_i\boldsymbol{v}_i^{n+1}(\nabla w_{ip})^T=\sum\limits_iw_{ip}\boldsymbol{v}_i^{n+1}((D_p^n)^{-1}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n))^T\]Though APIC(JCP-version): page 22, paragraph 1 said that
\[w_{ip}(D_p^n)^{-1}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n)=\nabla w_{ip}\]After my validation, this is not true. Perhaps it comes from assuming the velocity field is a affine veloctiy field
\[\boldsymbol{v}_q=\sum_iw_{iq}\boldsymbol{v}_i=\boldsymbol{v}_p+C_p^{n+1}(\boldsymbol{x}_q-\boldsymbol{x}_p)\]Differentiating this with respect to $\boldsymbol{x}_q$ goes to
\[\sum\limits_i\boldsymbol{v}_i(\nabla w_{iq})^T=C_p^{n+1}=\sum\limits_iw_{ip}\boldsymbol{v}_i^{n+1}((D_p^n)^{-1}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n))^T\]That is, for any point $q$, inside the supporting area, the velocity gradient equals to $C_p$.
MPM Scheme (explicit integration) #
- Initial values
- position of particle $\boldsymbol{x}_p^0$
- momentum of particle $m_p\boldsymbol{v}_p^0$
- deformation gradient of material point(particle) $F_p^0$
- affine matrix of particle $C_p^0$
- At time $t^n(n=0,1,2,…)$
- particle to grid
mass transfer
\[m_i=\sum_pw_{ip}m_p\]momentum transfer:
- add explicit internal force
calculate PK1 stress:
\[P_p^{n}=P_p(F_p^{n})\]calculate node force:
momentum update:
\[m_i\boldsymbol{\widetilde{v}}_i^{n+1}=m_i\boldsymbol{v}_i^{n}+\Delta t\boldsymbol{f}_i\]
add external force (e.g. gravity):
\[\boldsymbol{\widetilde{v}}_i^{n+1}=\boldsymbol{\widetilde{v}}_i^{n+1}+\boldsymbol{a}\Delta t\]- evolve deformation gradient
affine field:
\[C_p^{n+1}=(4/\Delta x^2)\sum_iw_{ip}\boldsymbol{\widetilde{v}}_i^{n+1}(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n)^T\]evolve deformation gradient:
grid to particle
- velocity:
advection:
\[\boldsymbol{x}_p^{n+1}=\boldsymbol{x}_p^{n}+\Delta t\boldsymbol{v}^{n+1}_p\]
- particle to grid