3D motion of rigid body
Moment of inertia #
Moment of inertia(转动惯量 $I$)是和mass(质量 $m$)类似的一个概念。
- $\boldsymbol{F}=m\boldsymbol{a}$,质量描述了力对物体产生加速效果的难易程度
- $\boldsymbol{\tau}=I\boldsymbol{\alpha}$,转动惯量描述了力矩对物体产生角加速度效果的难易程度
需要注意的是,虽然inertia和mass的概念非常相似,但是有所不同
- $m$描述了物体自身的性质。因此给定一个物体,它的$m$就定下来了
- $I$的测量除了给一个物体,还要指定旋转的转轴/参考点。
2D planar rigid body #
2D的旋转和3D的旋转是非常不同的。让我们先考虑2D的旋转。假设一个planar rigid body,他在绕轴 $\boldsymbol\omega$ 进行旋转。这根轴与rigid body的交点为 $G$。根据角动量的定义,我们可以得到关于G点的角动量$\boldsymbol{H_G}$
\[\boldsymbol{H_G}=\sum\limits_i(\boldsymbol{r_i}\times \boldsymbol{v_i} m_i)=\sum\limits_i(\boldsymbol{r_i}\times (\boldsymbol{\omega}\times\boldsymbol{r_i}) m_i)\]因为我们考虑的是2维的旋转,转轴 $\boldsymbol{\omega}$ 一定垂直于位矢 $\boldsymbol{r_i}$,因此$\boldsymbol{r_i}\times(\boldsymbol{\omega}\times\boldsymbol{r_i})=(\boldsymbol{r_i}\cdot\boldsymbol{r_i})\boldsymbol{\omega}$,因此
\[\boldsymbol{H_G}=\sum\limits_i(\boldsymbol{r_i}\times (\boldsymbol{\omega}\times\boldsymbol{r_i}) m_i)=\boldsymbol{\omega}\sum\limits_im_i(\boldsymbol{r_i}\cdot\boldsymbol{r_i})=I_G\boldsymbol{\omega}\]其中,$I_G$是关于G点的转动惯量,是一个标量。因此你可以观察到,在此处角速度和角动量的方向是一样的。
非惯性系 需要注意的是,我们现在的坐标系是定义在G上,也就是说,位矢是以G为原点,指向每一个质元的。如果我们的坐标原点 $G$ 是匀速运动的(相对于另一个惯性系),且坐标轴是不带旋转的,那么很显然,这个坐标系也是惯性系。但是有两种情况不同,
如果 $G$ 以加速度 $\boldsymbol{a}$ 变速运动,那么此时相对于G的坐标系是一个非惯性系,在进行力矩分析时,要引入惯性力。具体来说,惯性力产生的力矩为
\[\boldsymbol{\tau}=\sum\limits_i\boldsymbol{r_i}\times(-m_i\boldsymbol{a})=-\left(\sum\limits_i\boldsymbol{r_i}m_i\right)\times\boldsymbol{a}\]如果 $G$ 与质心 $CM$ 重合,则 $\sum\limits_i\boldsymbol{r_i}m_i=\boldsymbol{0}$,于是力矩为0,我们可以不考虑由惯性力产生的力矩对角动量产生的影响。
如果坐标系在绕着 $G$ 转动,那情况可就复杂的多了。具体的分析可以参考 《糕记理论力学》——03非惯性系。幸运的是,如果我们的坐标系是定义在body space的话(就像和刚体捆绑着一起运动),这样的情况下,由于刚体上的点相对与刚体捆绑的坐标系没有相对运动,因此不用考虑科里奥利力,只用考虑由坐标系变速平动产生的惯性力,和坐标系转动产生的离心力。由于离心力指向原点,因此不产生力矩。在这种情况下,我们的分析又回到了上一种情况。
因此,选择刚体的质心作为torque pivot进行运动分析会大大简化问题。选择其他的点虽然也能得出相同的结论,但要复杂得多。
3D rigid body #
当问题来到3D,情况一下子就变得复杂了。小二,上图 (出处)!

根据推导,转动惯量 $\boldsymbol{I_G}$ 现在不再是一个标量了!它变成了一个3x3的矩阵。如此,角动量 $\boldsymbol{H_G}$ 和角速度 $\boldsymbol{\omega}$ 甚至可能方向不同。但神奇的是,最后计算出来的角速度$\boldsymbol{\omega}$还是会和实际的转动保持一致的!让我们来看一个小例子。
假设一个质量为 $m$ 的小球在绕Z轴做匀速圆周运动,此刻它在XOZ平面上的位置为 $(1,0,2)$,速度为 $(0,v_y,0)$。我们可以发现,角动量的方向和角速度的方向是不一样的!但是它们通过一个转动惯量矩阵联系了起来!
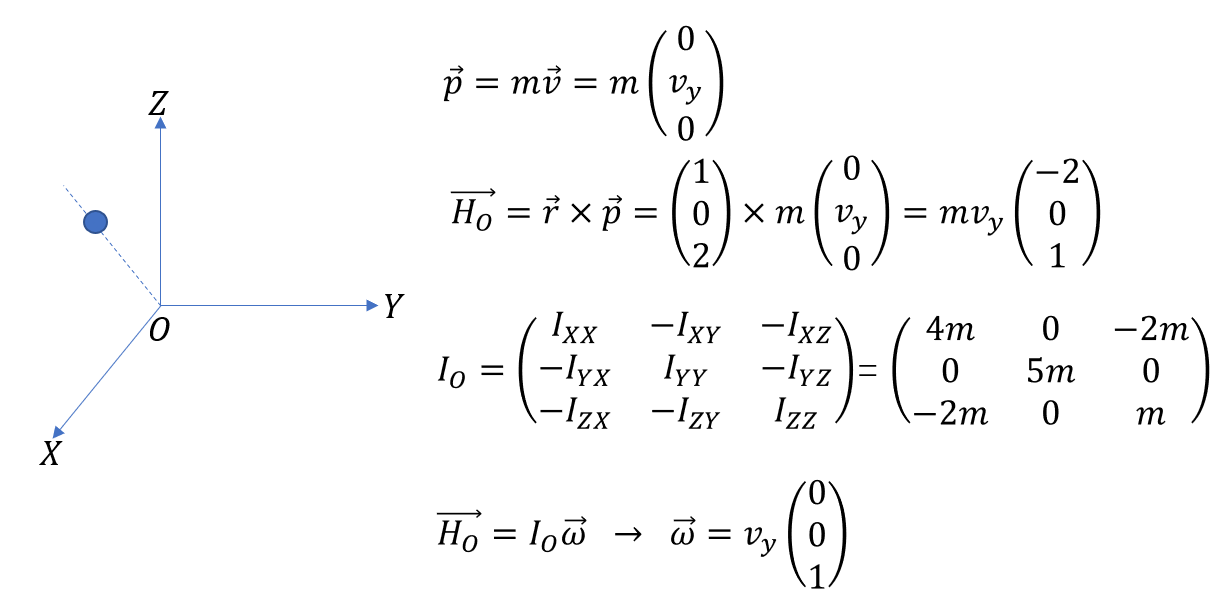
我们还注意到,上面的这张ppt中,$I_G$其实是会随着时间变化的。这是为什么呢?因为 $I_G$ 的三个轴实际上是和一个固定的惯性系OXYZ align的,而刚体在绕着G进行旋转,这就意味着,在不同的时间,同一个质元相对G的位矢 $\boldsymbol{r_i}$ 会发生变化,进而导致转动惯量改变。
如果认为在$t=0$时刻,G和O重合,IJK和XYZ重合。我们可以推出一个相对关系。假设位矢$\boldsymbol{r_i}$(相对于点O)
\[\boldsymbol{r_i}(t)=R(t)\boldsymbol{r_i}(0)+\boldsymbol{T}(t)\\ 令\ \boldsymbol{g_i}(t)=\boldsymbol{r_i}(t)-\boldsymbol{T}(t)=R(t)\boldsymbol{r_i}(0)\]其中,$\boldsymbol{g}_i$是相对于G的位矢,$R(t)$可以认为是相对于$R(0)$的旋转,我们可以令$R(0)={\rm identity}$,$\boldsymbol{T}(t)$是G点的位移,$\boldsymbol{T}(t)=\boldsymbol{0}$,则
\[\begin{align} I_G(t)&=\sum m_i\begin{bmatrix} g_{iy}^2+g_{iz}^2 & g_{ix}g_{iy} & -g_{ix}g_{iz} \\ -g_{ix}g_{iy} & g_{ix}^2+g_{iz}^2 & -g_{iy}g_{iz} \\ -g_{ix}g_{iz} & -g_{iy}g_{iz} & g_{ix}^2+g_{iy}^2 \end{bmatrix}\\ &=\sum m_i((\boldsymbol{g_i}^T\boldsymbol{g_i})\boldsymbol{1}-\boldsymbol{g_i}\boldsymbol{g_i}^T)\\ &=\sum m_i((R\boldsymbol{r_0})^T(R\boldsymbol{r_0})\boldsymbol{1}-(R\boldsymbol{r_0})(R\boldsymbol{r_0})^T)\\ &=\sum m_i((\boldsymbol{r_0}^T\boldsymbol{r_0})\boldsymbol{1}-R\boldsymbol{r_0}\boldsymbol{r_0}^TR^T) \end{align}\]由于$(\boldsymbol{r_0}^T\boldsymbol{r_0})\boldsymbol{1}$是标量x单位阵,因此可以等效成再乘一个单位阵$RR^T$,
\[I_G(t)=R(t)\left(\sum m_i(\boldsymbol{r_{i0}}^T\boldsymbol{r_{i0}})\boldsymbol{1}-\boldsymbol{r_{i0}}\boldsymbol{r_{i0}}^T\right)R(t)^T=R(t)I_OR(t)^T\]body space axes 如果我们一开始就把坐标系和body绑定在一起,那$I_G$就不会随着时间变化而变化,就像这样

但此时,由于坐标系实际上相对惯性系在旋转(可能还是变速的),就会产生上面说的非惯性系问题。
其中,向心加速度导致的力矩为
\[\sum\boldsymbol r_i\times m(\boldsymbol{\omega}\cdot(\boldsymbol\omega\cdot \boldsymbol r_i)-\boldsymbol\omega^2\boldsymbol r_i)=\sum m(\boldsymbol\omega\cdot \boldsymbol r_i)(\boldsymbol r_i\times \boldsymbol{\omega})\]太复杂了,不会算,分析到此为止x