APIC (Beginner Guide)
It’s been almost two years since I last wrote a blog. The reason I’m starting again is that I realized sometimes when I forget things, looking back at my own blog helps me recap very quickly. So I’m opening another recap log — this way, I can recap my recaps later on. And this time I will use LLM to polish my writing :)
Shape Functions #
The shape function $w_{ip}^n$ is associated with grid node $i$, and the particle position at time step $n$ is denoted by $\boldsymbol{x}_p^n$. We choose a shape function that satisfies the following conditions:
- Partition of unity
$\sum_i w_{ip}^n = 1$, but generally $\sum_p w_{ip}^n \neq 1$.
For example, if all particles are concentrated within a single cell, the corresponding nodes of that cell will accumulate large total weights.
- Linear consistency
Typical shape functions that meet these requirements include linear interpolation functions, barycentric coordinates, and B-splines.
Based on above properties, we can also derive that
\[\sum_i w_{ip}^n (\boldsymbol{x}_i^n - \boldsymbol{x}_p^n)=\boldsymbol{0}\]Momentums #
The total linear momentum on particles (before P2G)
\[\boldsymbol{p}_{tot}^{P,n}=\sum_p m_p\boldsymbol{v}_p^n\]The total linear momentum on the grid (after P2G)
\[\boldsymbol{p}_{tot}^{G,n}=\sum_i m_i^n\boldsymbol{v}_i^n\]The total angular momentum on the grid (after P2G)
\[\boldsymbol{L}_{tot}^{G,n}=\sum_i\boldsymbol{x}_i^n\times m_i^n\boldsymbol{v}_i^n\]The total linear momentum on the grid (after the grid dynamics, before G2P)
\[\boldsymbol{p}_{tot}^{G,n+1}=\sum_i m_i^n\boldsymbol{\tilde{v}}_i^{n+1}\]The total angular momentum on the grid (after the grid dynamics, before G2P)
\[\boldsymbol{L}_{tot}^{G,n+1}=\sum_i \boldsymbol{\tilde{x}}_i^{n+1}\times m_i^n\boldsymbol{\tilde{v}}_i^{n+1}\]When we consider conservation of angular momentum when transferring from grid to particles at the end of a time step, we need to consider angular momentum to be defined over moved grid nodes and we use the notation $\boldsymbol{\tilde{x}}_i^{n+1}=\boldsymbol{x}_i+\Delta t\boldsymbol{\tilde{v}}_i^{n+1}$ to indicate this.
One may notice that Eq. (5) gives
\[\boldsymbol{p}_{\mathrm{tot}}^{G,n+1} = \sum_i m_i^{n+1}\boldsymbol{v}_i^{n+1}, \notag\]while Eq. (7) defines it as
\[\boldsymbol{p}_{\mathrm{tot}}^{G,n+1} = \sum_i m_i^n\boldsymbol{\tilde{v}}_i^{n+1}. \notag\]A similar discrepancy can be observed between Eq. (6) and Eq. (8). Don’t worry! We will demonstrate the equivalence of these expressions in the following discussion.
RPIC (Rigid Particle-in-Cell) #
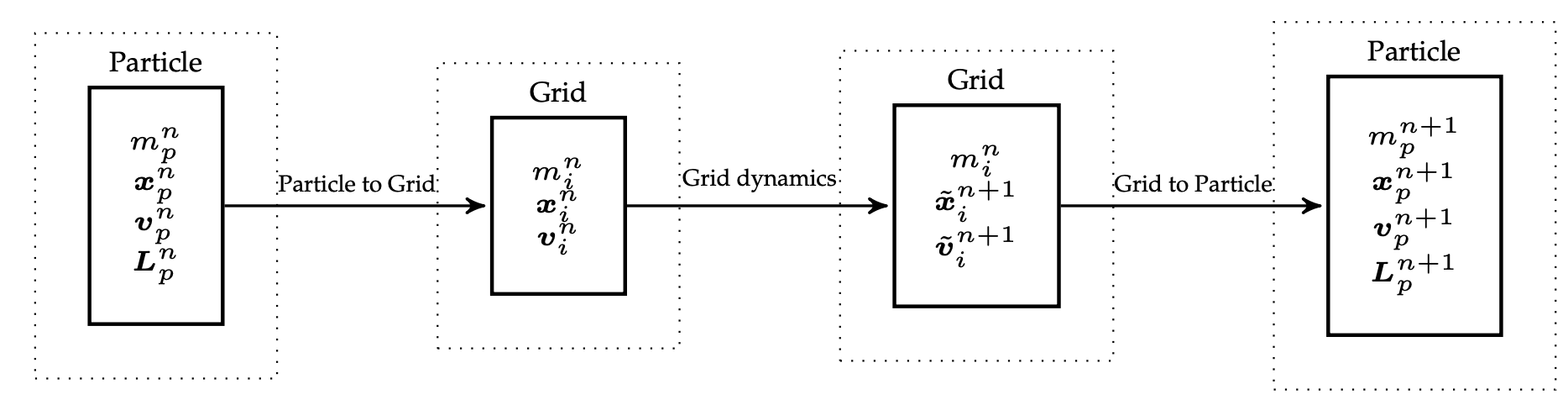
The transfer from particles to the grid are given by
\[\begin{align} m_i^n&=\sum_p w_{ip}^nm_p \notag\\ \boldsymbol{K}_p&=\sum_j w_{jp}^n m_p (\boldsymbol{x}_j^n-\boldsymbol{x}_p^n)^\star(\boldsymbol{x}_j^n-\boldsymbol{x}_p^n)^{\star T}\notag\\ m_i^n\boldsymbol{v}_i^n&=\sum_p w_{ip}^n m_p (\boldsymbol{v}_p^n + ((\boldsymbol{K}_p^n)^{-1}\boldsymbol{L}_p^n)\times(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n))\notag \end{align}\]One may imagine this transfer as distributing the masses $w_{ip}^n m_p$ from a rigid body to the grid node $i$. $\boldsymbol{K}_p$ is the inertia tensor associated with the local rigid body represented by particle $p$.
For any vectors $\boldsymbol{u}$ and $\boldsymbol{v}$, $\boldsymbol{u}^\star$ is defined to be the cross product matrix of $\boldsymbol{u}$, so that $\boldsymbol{u}^\star \boldsymbol{v}=\boldsymbol{u}\times\boldsymbol{v}$ and $(\boldsymbol{u}^\star)^T\boldsymbol{v}=\boldsymbol{v}\times\boldsymbol{u}$.
To be specific, the cross product matrix of a vector $\boldsymbol{u}$ is defined as
\[\boldsymbol{u}^\star = \begin{bmatrix} 0 & -u_z & u_y \\ u_z & 0 & -u_x \\ -u_y & u_x & 0 \end{bmatrix}.\notag\]Then,
\[\boldsymbol{u}^\star\boldsymbol{v} = \begin{bmatrix} 0 & -u_z & u_y \\ u_z & 0 & -u_x \\ -u_y & u_x & 0 \end{bmatrix} \begin{bmatrix} v_x \\[2pt] v_y \\[2pt] v_z \end{bmatrix} = \begin{bmatrix} u_y v_z - u_z v_y \\ u_z v_x - u_x v_z \\ u_x v_y - u_y v_x \end{bmatrix} = \boldsymbol{u} \times \boldsymbol{v}.\notag\]For Eq. (9), we have
\[\boldsymbol{r}^\star\boldsymbol{r}^{\star T} = \begin{bmatrix} 0 & -r_z & r_y \\ r_z & 0 & -r_x \\ -r_y & r_x & 0 \end{bmatrix} \begin{bmatrix} 0 & r_z & -r_y \\ -r_z & 0 & r_x \\ r_y & -r_x & 0 \end{bmatrix} = \begin{bmatrix} r_y^2 + r_z^2 & -r_x r_y & -r_x r_z \\ -r_x r_y & r_x^2 + r_z^2 & -r_y r_z \\ -r_x r_z & -r_y r_z & r_x^2 + r_y^2 \end{bmatrix}.\notag\]Therefore,
\[\begin{align} \boldsymbol{K}_p &= \sum_i w_{ip}^n m_i \begin{bmatrix} r_y^2 + r_z^2 & -r_x r_y & -r_x r_z \\ -r_x r_y & r_x^2 + r_z^2 & -r_y r_z \\ -r_x r_z & -r_y r_z & r_x^2 + r_y^2 \end{bmatrix} \notag\\ &\approx \begin{bmatrix} \int_m (r_y^2 + r_z^2)\, dm & \int_m (-r_x r_y)\, dm & \int_m (-r_x r_z)\, dm \\ \int_m (-r_x r_y)\, dm & \int_m (r_x^2 + r_z^2)\, dm & \int_m (-r_y r_z)\, dm \\ \int_m (-r_x r_z)\, dm & \int_m (-r_y r_z)\, dm & \int_m (r_x^2 + r_y^2)\, dm \end{bmatrix}= \begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{yx} & I_{yy} & -I_{yz} \\ -I_{zx} & -I_{zy} & I_{zz} \end{bmatrix} .\notag \end{align}\]
The transfer from the grid to particles are given by \(\begin{align} v_p^{n+1}&=\sum_i w_{ip}^n\boldsymbol{\tilde{v}}_i^{n+1} \notag\\ \boldsymbol{L}_p^{n+1}&=\sum_i w_{ip}^n(\boldsymbol{x}_i^n-\boldsymbol{x}_p^n)\times m_p\boldsymbol{\tilde{v}}_i^{n+1}\notag \end{align}\) The proofs for the preservation (or conservation) of the rigid-motion velocity field, linear momentum, and angular momentum are quite lengthy, so we will omit them here. For detailed derivations, please refer to the technical document of APIC. But basically, here are some take-away notes:
Preservation of the rigid-motion field
If the velocities before the transfer represent a rigid motion,
\[\boldsymbol{\tilde{v}}_i^{n+1} = \boldsymbol{v} + \boldsymbol{\omega} \times \boldsymbol{x}_i^n,\notag\]where $ \boldsymbol{v} $ and $ \boldsymbol{\omega} $ are constant vectors, then after G2P we have
\[\boldsymbol{v}_p^{n+1} = \boldsymbol{v} + \boldsymbol{\omega} \times \boldsymbol{x}_p^n.\notag\]The P2G operator also preserves this field.
Note that during G2P or P2G, since we typically use a B-spline kernel, each grid node or particle only exchanges physical quantities with its local $ 3\times3\times3 $ neighborhood. This means that in different $ 3\times3\times3 $ regions, the values of $ \boldsymbol{v} $ and $ \boldsymbol{\omega} $ can vary, as long as each local region represents a rigid-motion field.
Quadrature points with self-spin
Note that the total angular momentum on particles (before the particle-to-grid transfer at time $n$) represented by RPIC is
\[\boldsymbol{L}_{tot}^{P,G} = \sum_p (\boldsymbol{x}_p^n \times m_p \boldsymbol{v}_p^n + \boldsymbol{L}_p^n)\]At first glance, one might wonder why there is an additional term $ \boldsymbol{L}_p^n $ given that $ \boldsymbol{x}_p^n \times m_p \boldsymbol{v}_p^n $ already appears in the expression. The reason is that this is not a point particle—it is a quadrature point that represents a finite area (or volume). Therefore, the first term only accounts for the angular momentum of the center of mass, while the second term represents self-spin, capturing the rotational motion relative to the center of mass.
This also explains how we distribute the linear momentum from particles to the grid
\[m_i^n \boldsymbol{v}_i^n = \sum_p w_{ip}^n m_p \left( \boldsymbol{v}_p^n + ((\boldsymbol{K}_p^n)^{-1} \boldsymbol{L}_p^n) \times (\boldsymbol{x}_i^n - \boldsymbol{x}_p^n) \right) \notag\]The term $ ((\boldsymbol{K}_p^n)^{-1} \boldsymbol{L}_p^n) \times (\boldsymbol{x}_i^n - \boldsymbol{x}_p^n) $ represents the self-spinning velocity relative to the quadrature point’s center, which should be incorporated to correct the actual linear velocity during the transfer.