Multiview Correspondence

假设世界坐标系中有一个点$(X_w,Y_w,Z_w)$，首先变换到相机坐标系： \((X_c,Y_c,Z_c,1)^T=\rm{worldToCamera}\cdot(X_w,Y_w,Z_w,1)^T\) 因为这个变换只包含旋转和位移，因此齐次坐标的w部分不会改变，恒为1，也不需要做归一化，直接把矩阵乘法乘出来的齐次坐标的xyz拿过来用。

需要注意的是，Mitsuba中使用的相机坐标系的x/y轴与本文所使用的相机坐标系的x/y轴（下图中紫色的轴）相反，但都是右手系。Mitsuba的y轴与Lookat的up方向一致，而本文则是相反。本文受computer vision的影响，采用的相机坐标系的xy轴与最终图像的xy轴一致，因此在camera space到raster space的变换中不需要逆反xy轴。而Mitsuba则是将这个逆反放在了camera space到raster space的变换中。因此，区别只是在处理先后的问题。

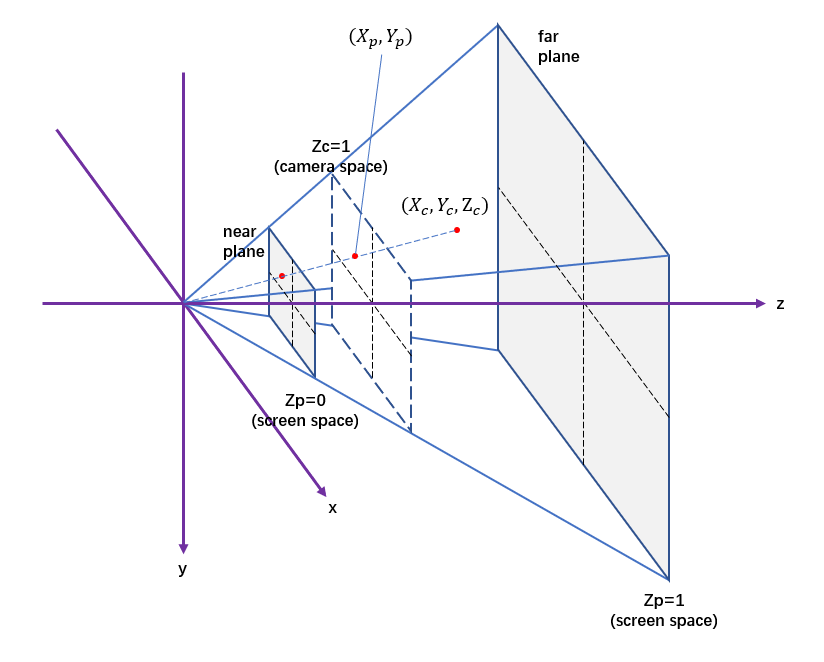
接着进行透视变换，首先以图形学中的perspective caemra为例：

mat4 perspectiveTransform(float fov, float nearz, float farz) {
  mat4 persp{nvmath::mat4f_zero};
  float recip = 1.0f / (farz - nearz);
  /* Perform a scale so that the field of view is mapped
   * to the interval [-1, 1] */
  float ctot = 1.0 / tanf(fov * nv_to_rad * 0.5);
  persp.a00 = 1; // ctot;
  persp.a11 = 1; // ctot;
  persp.a22 = farz * recip;
  persp.a23 = -nearz * farz * recip;
  persp.a32 = 1;
  return persp;
}

可以看到ctot被注释掉，我们等会儿来讨论来讨论他的作用。

现在，原来的点被变换到齐次坐标$(X_p’,Y_p’,Z_p’,W_p’)$：

因为是点的变换，所以最后出来的坐标实际上还要归一化。齐次坐标实际表示的三维空间中的点是$(X_p,Y_p,Z_p)$。

此时$(X_p,Y_p)$表示的是将点$(X_c,Y_c,Z_c)$投射到z=1的平面所产生的平面坐标。$Z_p$处于0和1之间，对应的是nearz和farz。

好，现在我们知道$(X_p,Y_p)$表示的是z=1平面上的坐标，根据fov (field of view，假设为$2\theta$)，我们就可以算出z=1平面上有效的窗口范围(clip window)。

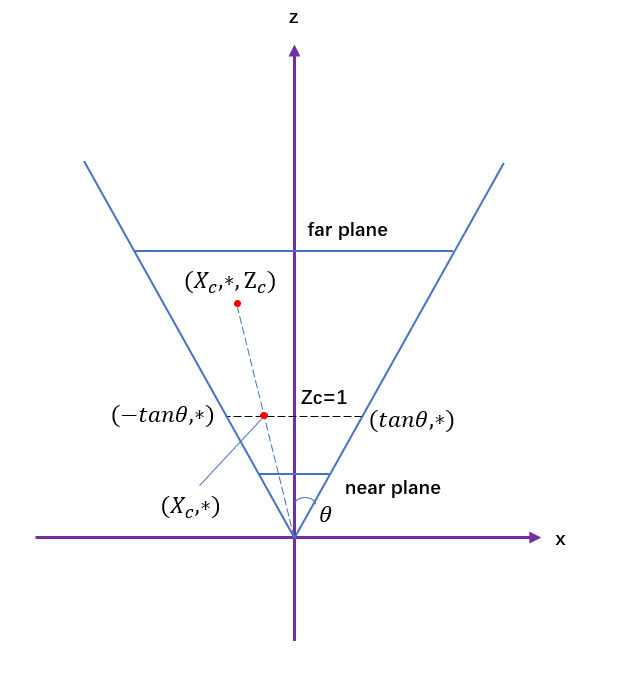
可以看到此时$X_p$的范围是$(-\rm{tan}\theta,\rm{tan}\theta)$。这里可以回想一下我们刚才把ctot注释掉了，如果考虑上ctot，那就是对x和y都做了一个 1/tan$\theta$ 的缩放，使得$X_p$的范围是$(-1,1)$。然后我们再考虑$Y_p$的范围。假设宽高比是aspect，高宽比是invAspect，则$Y_p$的范围是$(-\rm{invAspect,invAspect})$。

然后再来看相机空间到光栅化空间的变换：

mat4 cameraToRasterTransform(VkExtent2D filmSize, float fov, float near,
                             float far) {
  float aspect = filmSize.width / float(filmSize.height);
  float invAspect = 1.f / aspect;
  // This gives a transformation from camera space to screen space.
  // In x this space ranges from -1 to 1 but y ranges from -invAspect
  // to invAspect, since aspect ratio is not taken into account.
  mat4 cameraToScreen = perspectiveTransform(fov, near, far);
  // x and y ranges from (-1,1) x (-1,1)
  cameraToScreen = nvmath::scale_mat4(vec3(1.f, aspect, 1.f)) * cameraToScreen;
  // x and y ranges from (0,2) x (0,2)
  cameraToScreen =
      nvmath::translation_mat4(vec3(1.f, 1.f, 0.f)) * cameraToScreen;
  // x and y ranges from (0,1) x (0,1)
  mat4 cameraToNdc =
      nvmath::scale_mat4(vec3(0.5f, 0.5f, 1.f)) * cameraToScreen;
  // x and y ranges from (0,0) to (width,height)
  mat4 cameraToRaster =
      nvmath::scale_mat4(vec3(filmSize.width, filmSize.height, 1.f)) *
      cameraToNdc;
  return cameraToRaster;
}

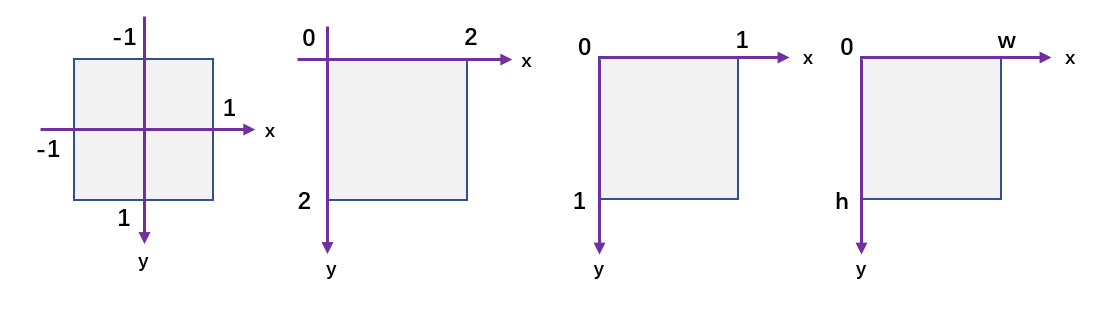
cameraToScreen就是我们之前讲的变换。之后我们将screen space变换到raster space：首先都缩放到$(-1,1)$也就是ndc空间，紧接着在y方向上平移了1，在x方式上平移了1，然后进行了一个缩放；ndc space和screen space没啥区别，唯一的区别就是，ndc空间的xy范围都是-1到1。

ndc到raster空间的变化如图所示。

现在总算知道之前写Asuna渲染器的时候怪在哪儿了。Asuna（当前版本）里面，Loader载入的shot中的up向量，用它来算Lookat的时候，产生的worldToCamera变换会使得相机的y轴和up重合。这其实也挺合理的，因为从相机最后拍摄得到的图像来看，up就是上面嘛~哪有说y和up是反着的。但是vision那边，相机的y轴和图像的y轴重合，指向地面orz，怪不得之前怎么写怎么不对劲呢。

那想清楚了之后怎么设计才会比较优雅呢？现在比较麻的一点是因为要用现有的view更新框架（这样gui操作比较方便），perspective camera中直接套用了nvpro_core的camera，但是这个camera space的y是和up重合的，x指向右侧，z指向backward。

好像也挺简单的，就是把y和z的方向都反一下，就变成我第一幅图中所画的相机坐标系了。

  mat4 getView() {
    return nvmath::scale_mat4(vec3(1.f, -1.f, -1.f)) * CameraManip.getMatrix();
  }

然后现在还有个怎么都写不对的两相机correspondence。基本的思路就是：

• 目标是寻找reference view中某个pixel在source view中的对应
• 思路：
  1. 从reference pixel射出射线与场景相交于点p
  2. 检查点p到source camera的射线是否会被遮挡
  3. 如果被遮挡就说明在source view中看不到该点
  4. 没被遮挡就运用worldToRaster找到source view中的对应像素

我怎么想都觉得思路肯定没错，明天再看看吧（写于2022/6/18

擦，今天（2022/6/19）终于发现错在哪儿了。一路下来到生成对应像素的flow、存到图片都没有错。错的是，可视化的时候，用的是opencv读flow，会把RGB channel反一下，导致了我flow valid（我存在B通道，结果用了R通道）判断错误。正确的结果如下：