APIC (Beginner Guide)

It’s been almost two years since I last wrote a blog. The reason I’m starting again is that I realized sometimes when I forget things, looking back at my own blog helps me recap very quickly. So I’m opening another recap log — this way, I can recap my recaps later on. And this time I will use LLM to polish my writing :)

Shape Functions #

The shape function $w_{ip}^n$ is associated with grid node $i$, and the particle position at time step $n$ is denoted by $\boldsymbol{x}_p^n$. We choose a shape function that satisfies the following conditions:

• Partition of unity

$\sum_i w_{ip}^n = 1$, but generally $\sum_p w_{ip}^n \neq 1$.
For example, if all particles are concentrated within a single cell, the corresponding nodes of that cell will accumulate large total weights.

• Linear consistency

Typical shape functions that meet these requirements include linear interpolation functions, barycentric coordinates, and B-splines.

Based on above properties, we can also derive that

Momentums #

The total linear momentum on particles (before P2G)

The total linear momentum on the grid (after P2G)

The total angular momentum on the grid (after P2G)

The total linear momentum on the grid (after the grid dynamics, before G2P)

The total angular momentum on the grid (after the grid dynamics, before G2P)

When we consider conservation of angular momentum when transferring from grid to particles at the end of a time step, we need to consider angular momentum to be defined over moved grid nodes and we use the notation $\boldsymbol{\tilde{x}}_i^{n+1}=\boldsymbol{x}_i+\Delta t\boldsymbol{\tilde{v}}_i^{n+1}$ to indicate this.

One may notice that Eq. (5) gives

while Eq. (7) defines it as

A similar discrepancy can be observed between Eq. (6) and Eq. (8). Don’t worry! We will demonstrate the equivalence of these expressions in the following discussion.

RPIC (Rigid Particle-in-Cell) #

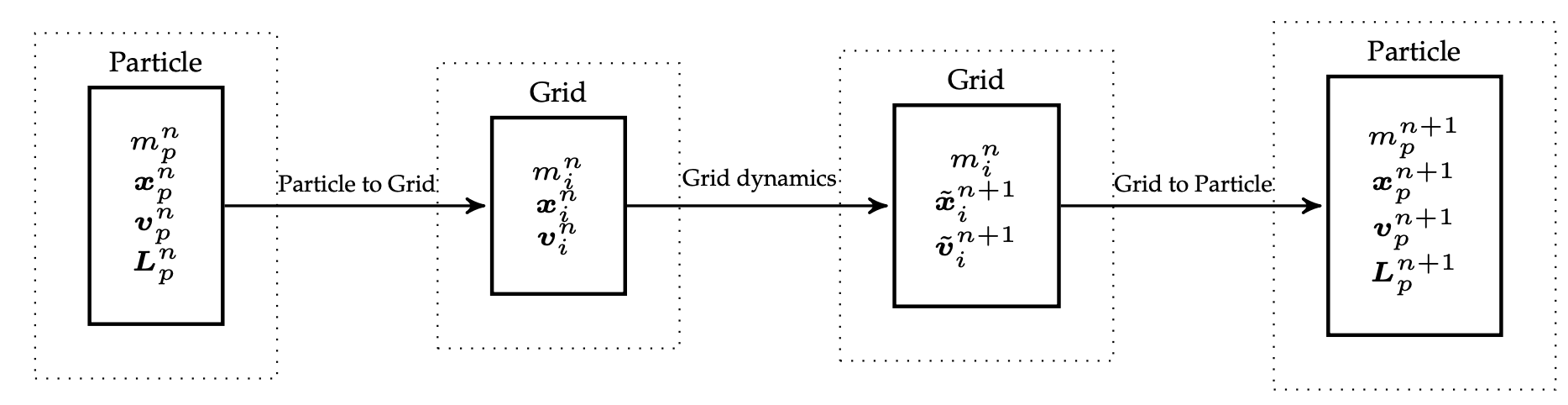
The transfer from particles to the grid are given by

One may imagine this transfer as distributing the masses $w_{ip}^n m_p$ from a rigid body to the grid node $i$. $\boldsymbol{K}_p^n$ is the inertia tensor associated with the local rigid body represented by particle $p$.

For any vectors $\boldsymbol{u}$ and $\boldsymbol{v}$, $\boldsymbol{u}^\star$ is defined to be the cross product matrix of $\boldsymbol{u}$, so that $\boldsymbol{u}^\star \boldsymbol{v}=\boldsymbol{u}\times\boldsymbol{v}$ and $(\boldsymbol{u}^\star)^\top\boldsymbol{v}=\boldsymbol{v}\times\boldsymbol{u}$.

To be specific, the cross product matrix of a vector $\boldsymbol{u}$ is defined as

\[\boldsymbol{u}^\star = \begin{bmatrix} 0 & -u_z & u_y \\ u_z & 0 & -u_x \\ -u_y & u_x & 0 \end{bmatrix}.\notag\]

Then,

\[\boldsymbol{u}^\star\boldsymbol{v} = \begin{bmatrix} 0 & -u_z & u_y \\ u_z & 0 & -u_x \\ -u_y & u_x & 0 \end{bmatrix} \begin{bmatrix} v_x \\[2pt] v_y \\[2pt] v_z \end{bmatrix} = \begin{bmatrix} u_y v_z - u_z v_y \\ u_z v_x - u_x v_z \\ u_x v_y - u_y v_x \end{bmatrix} = \boldsymbol{u} \times \boldsymbol{v}.\notag\]

For Eq. (9), we have

\[\boldsymbol{r}^\star\boldsymbol{r}^{\star \top} = \begin{bmatrix} 0 & -r_z & r_y \\ r_z & 0 & -r_x \\ -r_y & r_x & 0 \end{bmatrix} \begin{bmatrix} 0 & r_z & -r_y \\ -r_z & 0 & r_x \\ r_y & -r_x & 0 \end{bmatrix} = \begin{bmatrix} r_y^2 + r_z^2 & -r_x r_y & -r_x r_z \\ -r_x r_y & r_x^2 + r_z^2 & -r_y r_z \\ -r_x r_z & -r_y r_z & r_x^2 + r_y^2 \end{bmatrix}.\notag\]

Therefore,

\[\begin{align} \boldsymbol{K}_p^n &= \sum_i w_{ip}^n m_i^n \begin{bmatrix} r_y^2 + r_z^2 & -r_x r_y & -r_x r_z \\ -r_x r_y & r_x^2 + r_z^2 & -r_y r_z \\ -r_x r_z & -r_y r_z & r_x^2 + r_y^2 \end{bmatrix} \notag\\ &\approx \begin{bmatrix} \int_m (r_y^2 + r_z^2)\, dm & \int_m (-r_x r_y)\, dm & \int_m (-r_x r_z)\, dm \\ \int_m (-r_x r_y)\, dm & \int_m (r_x^2 + r_z^2)\, dm & \int_m (-r_y r_z)\, dm \\ \int_m (-r_x r_z)\, dm & \int_m (-r_y r_z)\, dm & \int_m (r_x^2 + r_y^2)\, dm \end{bmatrix}= \begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{yx} & I_{yy} & -I_{yz} \\ -I_{zx} & -I_{zy} & I_{zz} \end{bmatrix} .\notag \end{align}\]

The transfer from the grid to particles are given by

The proofs for the preservation (or conservation) of the rigid-motion velocity field, linear momentum, and angular momentum are quite lengthy, so we will omit them here. For detailed derivations, please refer to the technical document of APIC. But basically, here are some take-away notes:

• Preservation of the rigid-motion field

  If the velocities before the transfer represent a rigid motion,

  \[\boldsymbol{\tilde{v}}_i^{n+1} = \boldsymbol{v} + \boldsymbol{\omega} \times \boldsymbol{x}_i^n,\notag\]

  where $ \boldsymbol{v} $ and $ \boldsymbol{\omega} $ are constant vectors, then after G2P we have

  \[\boldsymbol{v}_p^{n+1} = \boldsymbol{v} + \boldsymbol{\omega} \times \boldsymbol{x}_p^n.\notag\]

  The P2G operator also preserves this field.

  Note that during G2P or P2G, since we typically use a B-spline kernel, each grid node or particle only exchanges physical quantities with its local $ 3\times3\times3 $ neighborhood. This means that in different $ 3\times3\times3 $ regions, the values of $ \boldsymbol{v} $ and $ \boldsymbol{\omega} $ can vary, as long as each local region represents a rigid-motion field.

• Quadrature points with self-spin

  Note that the total angular momentum on particles (before the particle-to-grid transfer at time $n$) represented by RPIC is

  \[\boldsymbol{L}_{tot}^{P,G} = \sum_p (\boldsymbol{x}_p^n \times m_p \boldsymbol{v}_p^n + \boldsymbol{L}_p^n)\]

  At first glance, one might wonder why there is an additional term $ \boldsymbol{L}_p^n $ given that $ \boldsymbol{x}_p^n \times m_p \boldsymbol{v}_p^n $ already appears in the expression. The reason is that this is not a point particle—it is a quadrature point that represents a finite area (or volume). Therefore, the first term only accounts for the angular momentum of the center of mass, while the second term represents self-spin, capturing the rotational motion relative to the center of mass.

  This also explains how we distribute the linear momentum from particles to the grid

  \[m_i^n \boldsymbol{v}_i^n = \sum_p w_{ip}^n m_p \left( \boldsymbol{v}_p^n + ((\boldsymbol{K}_p^n)^{-1} \boldsymbol{L}_p^n) \times (\boldsymbol{x}_i^n - \boldsymbol{x}_p^n) \right) \notag\]

  The term $ ((\boldsymbol{K}_p^n)^{-1} \boldsymbol{L}_p^n) \times (\boldsymbol{x}_i^n - \boldsymbol{x}_p^n) $ represents the self-spinning velocity relative to the quadrature point’s center, which should be incorporated to correct the actual linear velocity during the transfer.

APIC (Affine Particle-in-Cell) #

APIC is quite similar to RPIC. However, instead of recovering a rigid motion field, it takes one step further — we now recover an affine motion field

Here, $ \boldsymbol{C} $ is a matrix. The transfer from particles to the grid is given by

The transfer back to particles is given by

Analogous to how the angular velocity $ \boldsymbol{\omega} $ can be reconstructed via $ \boldsymbol{\omega} = \boldsymbol{K}^{-1} \boldsymbol{L} $ — where $ \boldsymbol{K} $ is the inertia tensor and $ \boldsymbol{L} $ is the angular momentum — we may ask how $ \boldsymbol{C} $ can be reconstructed.

Is there an invariant quantity that characterizes $ \boldsymbol{C} $, similar to how the inertia tensor describes angular motion? Indeed, there is — it is captured by $ \boldsymbol{B} $ and $ \boldsymbol{D} $.

• Minimal least squares for $ \boldsymbol{B} $ and $ \boldsymbol{D} $

  One might wonder where $ \boldsymbol{B} $ and $ \boldsymbol{D} $ come from. We will derive them through a specific example and show that the resulting formula preserves both overall momentum and angular momentum.

  Suppose we have only one particle (or equivalently, one quadrature point). Its underlying quadrature is represented by a grid ${\boldsymbol{x}_i}$. The particle has a position $\boldsymbol{x}_p$. Given that the affine motion is described by

  \[\boldsymbol{v}(\boldsymbol{x}) = \boldsymbol{v}_p + \boldsymbol{C}_p (\boldsymbol{x} - \boldsymbol{x}_p), \quad \forall \boldsymbol{x} \in \text{quadrature},\]

  which also holds for each grid node $i$. Assume the velocity associated with node $i$ is $\boldsymbol{v}_i$. We want the momentum stored in the affine motion field to best approximate the momentum on the grid. That is, we aim to solve for $ \boldsymbol{C}_p $ and $ \boldsymbol{v}_p $ from

  \[\mathop{\rm argmin}_{\boldsymbol{C}_p, \boldsymbol{v}_p} \sum_i \left\| w_{ip} m_p [\boldsymbol{v}_p + \boldsymbol{C}_p (\boldsymbol{x}_i - \boldsymbol{x}_p)] - \sum_i m_i \boldsymbol{v}_i \right\|^2\]

  We already know that the mass on the quadrature represented by grid node $i$ is $ w_{ip} m_p $ (some confusion might arise here; the key takeaway is that we can imagine a quadrature point as an equivalent grid element describing an area or volume. Even though we only have one particle, we store certain physical quantities on it, such as $ \boldsymbol{C} $, and these quantities are later transferred to the grid during the P2G step).

  Therefore, Eq. (11) becomes

  \[\mathop{\rm argmin}_{\boldsymbol{C}_p, \boldsymbol{v}_p} \sum_i \left\| w_{ip} m_p [\boldsymbol{v}_p + \boldsymbol{C}_p (\boldsymbol{x}_i - \boldsymbol{x}_p)] - \sum_i w_{ip} m_p \boldsymbol{v}_i \right\|^2 \notag\]

  Since $ m_p $ is a constant, we can drop it and denote the error as $ E $:

  \[\begin{align} \mathop{\rm argmin}_{\boldsymbol{C}_p, \boldsymbol{v}_p} E(\boldsymbol{C}_p, \boldsymbol{v}_p) &= \mathop{\rm argmin}_{\boldsymbol{C}_p, \boldsymbol{v}_p} \sum_i \left\| w_{ip} [\boldsymbol{v}_p + \boldsymbol{C}_p (\boldsymbol{x}_i - \boldsymbol{x}_p)] - \sum_i w_{ip} \boldsymbol{v}_i \right\|^2 \notag \\ &= \mathop{\rm argmin}_{\boldsymbol{C}_p, \boldsymbol{v}_p} [\boldsymbol{v}_p + \boldsymbol{C}_p (\boldsymbol{x}_i - \boldsymbol{x}_p)]^\top [\boldsymbol{v}_p + \boldsymbol{C}_p (\boldsymbol{x}_i - \boldsymbol{x}_p)] \end{align}\]

  To find the minimum, we take derivatives of $ E $ with respect to $ \boldsymbol{C}_p $ and $ \boldsymbol{v}_p $, and set them to zero:

  \[\frac{\partial E}{\partial \boldsymbol{C}_p} = 2 \sum_i w_{ip} (\boldsymbol{v}_p + \boldsymbol{C}_p \boldsymbol{r}_i - \boldsymbol{v}_i) \boldsymbol{r}_i^\top = 0\] \[\frac{\partial E}{\partial \boldsymbol{v}_p} = 2 \sum_i w_{ip} (\boldsymbol{v}_p + \boldsymbol{C}_p \boldsymbol{r}_i - \boldsymbol{v}_i) = 0\]

  Since we have \(\sum_i w_{ip} = 1\notag\) and \(\sum_i w_{ip} (\boldsymbol{x}_i - \boldsymbol{x}_p) = \boldsymbol{0},\notag\) from Eq. (14) we obtain

  \[\boldsymbol{v}_p = \sum_i w_{ip} \boldsymbol{v}_i.\]

  From Eq. (13), we get

  \[\sum_i w_{ip} (\boldsymbol{v}_i - \boldsymbol{v}_p) \boldsymbol{r}_i^\top = \boldsymbol{C}_p \sum_i w_{ip} \boldsymbol{r}_i \boldsymbol{r}_i^\top.\]

  Denoting

  \[\boldsymbol{D}_p = \sum_i w_{ip} \boldsymbol{r}_i \boldsymbol{r}_i^\top\]

  and

  \[\boldsymbol{B}_p = \sum_i w_{ip} (\boldsymbol{v}_i - \boldsymbol{v}_p) \boldsymbol{r}_i^\top,\]

  we finally have

  \[\boldsymbol{C}_p = \boldsymbol{B}_p (\boldsymbol{D}_p)^{-1}.\notag\]

• Grid averaging effect

  The derivation above applies to a single particle. When we have many particles, even if each particle is initially assigned a distinct affine motion $ \boldsymbol{C}_p $, after the P2G transfer, each grid node is influenced by multiple particles. As a result, the grid effectively represents an average affine motion field across those particles. Consequently, during the subsequent G2P transfer, the affine motion field reconstructed for each quadrature point will no longer match its previous state exactly.

  However, if we begin from the grid — where the affine motion field is already stored — and perform G2P, each resulting particle will still represent an affine motion consistent with the others. After performing P2G again, the grid recovers the same affine motion field.

  The key takeaway is that different particles should not carry significantly different affine motions. Otherwise, these variations will be averaged out on the grid during P2G and cannot be maintained across transfers.

• Conservation of momentum

  The good news is that, despite this averaging effect, the total linear and angular momentum of the system remain conserved. For detailed proof, please refer to the technical document of APIC.

  The total angular momentum on particles represented by APIC is given by

  \[\boldsymbol{L}_{tot}^{P,n} = \sum_p \boldsymbol{x}_p \times (m_p \boldsymbol{v}_p) + \sum_p m_p (\boldsymbol{B}_p^n)^\top : \boldsymbol{\epsilon}\]

  Here, we use the permutation tensor $ \boldsymbol{\epsilon} $ to convert a cross product into a tensor contraction. Specifically,

  \[\boldsymbol{u} \times \boldsymbol{v} = (\boldsymbol{v} \boldsymbol{u}^\top)^\top : \boldsymbol{\epsilon}\]

  For a matrix $ \boldsymbol{A} = { A_{\alpha\beta} } $, we have

  \[(\boldsymbol{A} : \boldsymbol{\epsilon})_\gamma = \sum_{\alpha, \beta} A_{\alpha\beta} \epsilon_{\alpha\beta\gamma}\]

  For a $ 3 \times 3 $ matrix, this expands to

  \[\begin{align} (\boldsymbol{A} : \boldsymbol{\epsilon})_1 &= A_{23} - A_{32} \notag\\ (\boldsymbol{A} : \boldsymbol{\epsilon})_2 &= A_{31} - A_{13} \notag\\ (\boldsymbol{A} : \boldsymbol{\epsilon})_3 &= A_{12} - A_{21} \notag \end{align}\]

  Therefore,

  \[(\boldsymbol{v} \boldsymbol{u}^\top)^\top : \boldsymbol{\epsilon} = \begin{bmatrix} u_1 v_1 & u_1 v_2 & u_1 v_3 \notag\\ u_2 v_1 & u_2 v_2 & u_2 v_3 \notag\\ u_3 v_1 & u_3 v_2 & u_3 v_3 \notag \end{bmatrix} : \boldsymbol{\epsilon} = \begin{pmatrix} u_2 v_3 - u_3 v_2 \\ u_3 v_1 - u_1 v_3 \\ u_1 v_2 - u_2 v_1 \end{pmatrix} = \boldsymbol{u} \times \boldsymbol{v}\]

  Since

  \[\boldsymbol{B}_p = \sum_i w_{ip} (\boldsymbol{v}_i - \boldsymbol{v}_p) \boldsymbol{r}_i^\top,\notag\]

  we have

  \[\begin{align} \sum_p m_p (\boldsymbol{B}_p^n)^\top : \boldsymbol{\epsilon} &= \sum_p m_p \left[ \sum_i (\boldsymbol{v}_i - \boldsymbol{v}_p) \boldsymbol{r}_i^\top \right]^\top : \boldsymbol{\epsilon} \notag\\ &= \sum_{i,p} m_p [(\boldsymbol{v}_i - \boldsymbol{v}_p) \boldsymbol{r}_i^\top]^\top : \boldsymbol{\epsilon} \notag\\ &= \sum_{i,p} m_p \boldsymbol{r}_i \times (\boldsymbol{v}_i - \boldsymbol{v}_p) \notag \end{align}\]

  This explains the presence of the second term in the total angular momentum expression.

• Constant $ \boldsymbol{D} $

  There is another good piece of news. The formula

  \[\boldsymbol{D}_p^n = \sum_i w_{ip}^n (\boldsymbol{x}_i^n - \boldsymbol{x}_p^n)(\boldsymbol{x}_i^n - \boldsymbol{x}_p^n)^\top \notag\]

  can be simplified. For the quadratic B-spline kernel,

  \[w(r) = \begin{cases} \dfrac{3}{4} - r^2, & |r| < \dfrac{1}{2}, \\[6pt] \dfrac{1}{2}\left(\dfrac{3}{2} - |r|\right)^2, & \dfrac{1}{2} \le |r| < \dfrac{3}{2}, \\[6pt] 0, & |r| \ge \dfrac{3}{2}. \end{cases}\notag\] \[\begin{align} \boldsymbol{D}_p^n &= \sum_i w_{ip}^n \begin{pmatrix} \boldsymbol{r}_1 \Delta x \\ \boldsymbol{r}_2 \Delta x \end{pmatrix} \begin{pmatrix} \boldsymbol{r}_1 \Delta x & \boldsymbol{r}_2 \Delta x \end{pmatrix} \notag\\ &= \Delta x^2 \sum_i w_{ip}^n \begin{pmatrix} \boldsymbol{r}_1 \\ \boldsymbol{r}_2 \end{pmatrix} \begin{pmatrix} \boldsymbol{r}_1 & \boldsymbol{r}_2 \end{pmatrix} \notag \end{align}\]

  This quantity is constant and invariant to geometry or kernel. Instead of deriving it analytically, we can confirm this numerically with the following code:

  import numpy as np
  def quadratic_b_spline(r):
      if abs(r) < 0.5: return 0.75 - r**2
      elif abs(r) < 1.5: return 0.5 * (1.5 - abs(r))**2
      else: return 0.0
    
  def cubic_b_spline(r):
      if abs(r) < 1.0: return 4/6 - r**2 + 0.5 * abs(r)**3
      elif abs(r) < 2.0: return ((2 - abs(r))**3) / 6
      else: return 0.0
    
  x = np.linspace(-3, 3, 7)
  x, y, z = np.meshgrid(x, x, x)
  x = np.stack([x, y, z], -1).reshape(-1, 3)
  dx = 1
  kernel = cubic_b_spline  # or quadratic_b_spline
  xp = np.random.uniform(-0.5, 0.5, (3))
  Dp = np.zeros((3, 3))
  for xi in x:
      ri = xi - xp
      wip = np.array([kernel(ri[_] / dx) for _ in range(3)])
      wip = np.prod(wip)
      Dp += wip * (ri[:, None] @ ri[None, :])
  Dp
  

  For the cubic kernel

  array([[ 3.33333333e-01, -1.08149167e-17,  8.94466792e-19],
         [-1.08149167e-17,  3.33333333e-01, -1.13841228e-17],
         [ 8.94466792e-19, -1.13841228e-17,  3.33333333e-01]])
  

  which is $\frac{1}{3}\Delta x^2$. For the quadratic kernel

  array([[ 2.50000000e-01, -2.94767466e-18, -2.60208521e-18],
         [-2.94767466e-18,  2.50000000e-01,  9.74426703e-18],
         [-2.60208521e-18,  9.74426703e-18,  2.50000000e-01]])
  

  which is $\frac{1}{4}\Delta x^2$. So we have

  \[\begin{align} \boldsymbol{C}_p^{n+1} &= \boldsymbol{B}_p^{n+1} (\boldsymbol{D}_p^{n+1})^{-1}.\notag\\ &=\frac{4}{\Delta x^2}\sum_i w_{ip}^n \boldsymbol{\tilde{v}}_i^{n+1} (\boldsymbol{x}_i^n - \boldsymbol{x}_p^n)^\top \end{align}\]

  for quadratic kernel.

MLS-MPM #

For weak form, evolve of internal force,